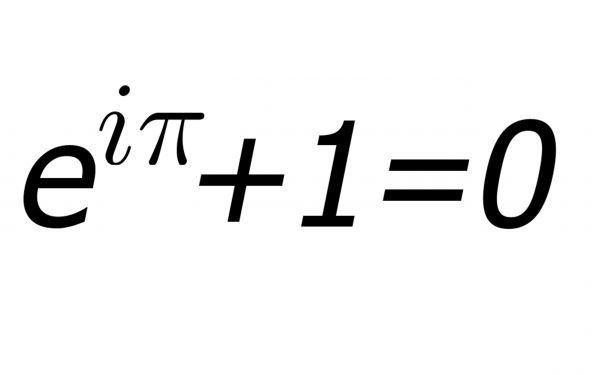
Las matemáticas son una de las únicas áreas de conocimiento que objetivamente pueden describirse como «verdaderas», porque sus teoremas se derivan de la lógica pura. Y, sin embargo, al mismo tiempo, esos teoremas suelen ser extremadamente extraños y contrarios a la intuición.
Algunas personas encuentran aburridas las matemáticas. Como muestran estos ejemplos, es todo menos eso:
- Patrones aleatorios
Curiosamente, los datos aleatorios no son en realidad tan aleatorios. En una lista dada de números que representan cualquier cosa, desde el precio de las acciones hasta la población de la ciudad, la altura de los edificios y la longitud de los ríos, alrededor del 30 por ciento de los números comenzarán con el dígito 1. Menos de ellos comenzarán con 2, incluso menos con 3 , y así sucesivamente, hasta que solo un número de cada veinte comience con un 9. Cuanto más grande sea el conjunto de datos y más órdenes de magnitud se extienda, más fuertemente emerge este patrón. - Espirales primas
Debido a que los números primos son indivisibles (excepto por 1 y ellos mismos), y debido a que todos los demás números pueden escribirse como múltiplos de ellos, a menudo se los considera como los «átomos» del mundo matemático. A pesar de su importancia, la distribución de los números primos entre los enteros sigue siendo un misterio. No hay un patrón que dicte qué números serán primos o qué tan separados estarán los números primos sucesivos. - Eversión de la esfera
En un campo importante de las matemáticas llamado topología, dos objetos se consideran equivalentes, o «homeomórficos», si uno puede transformarse en el otro simplemente girando y estirando su superficie; son diferentes si tienes que cortar o doblar la superficie de uno para darle la forma del otro. - Patrones geométricos
Aunque pueden estar decorados con una variedad infinita de florituras, matemáticamente hablando, solo hay un número finito de patrones geométricos distintos. Todas las pinturas, papeles pintados, diseños de azulejos de Escher y, de hecho, todos los arreglos bidimensionales repetidos de formas pueden identificarse como pertenecientes a uno u otro de los denominados «grupos de papeles pintados». ¿Y cuántos grupos de fondos de pantalla hay? Exactamente 17. - El soneto de Euler
«Como un soneto de Shakespeare que captura la esencia misma del amor, o una pintura que resalta la belleza de la forma humana que es mucho más que superficial, la Ecuación de Euler llega hasta las profundidades de la existencia».
El matemático de Stanford Keith Devlin escribió estas palabras sobre la ecuación de Euler (al principio del post), en un ensayo de 2002 titulado «La ecuación más hermosa».